Transformer神经网络基础

函数：描述了一种输入与输出之间的映射关系

\begin{aligned} \text{线性函数}:&f(x)=wx+b,\ w\text{是权重，}b\text{是偏置}\\ \text{激活函数}:&f(x)=g(wx+b)\\ \text{常用的激活函数}:&g(x)=\frac{1}{1+e^{-z}},\ \text{ReLU}(z)=\max(0,z) \end{aligned}

由于数据分布不均匀时，线性函数无法拟合真实数据，需要使用非线性函数。在线性函数外层套一层激活函数，就可以将原本的线性函数变成表达能力更强的非线性函数。

神经网络

f(x)=g(wx+b)

只有一个输入时如上式。输入变多后：

f(x)=g(w_1x_1+w_2x_2+b)

在原函数基础上再套一层激活函数：

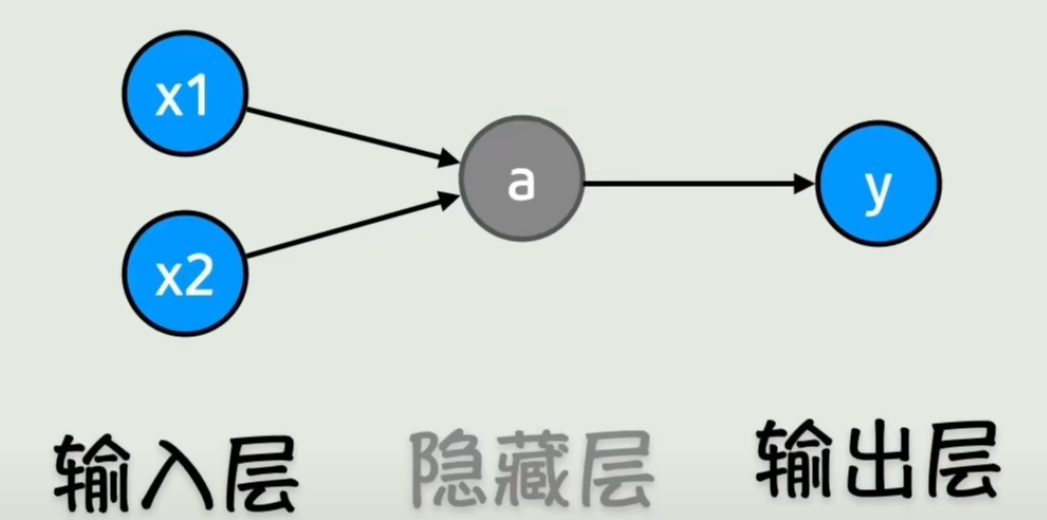
f(x)=g\bigl(w_3(g(w_1x_1+w_2x_2+b))+b\bigr)

\begin{aligned} f(x)&=g(w_3f_1(x)+b)\\ f_1(x)&=g(w_1x_1+w_2x_2+b)=y \end{aligned}

此时 $f_1$ 这一层就称为隐藏层。

由大量神经元组成的网络结构，我们称之为神经网络。

前向传播：在神经网络中从左到右、从输入到输出，逐步计算函数值的过程。

判断神经网络训练好坏，就是看它与真实数据的拟合程度。

用数学语言描述拟合好坏：已知 $f(x)=wx+b$ ，我们希望求出合适的 $w$ 和 $b$ 。每个数据点上，竖直方向的长度就是真实值与预测值之间的误差。将所有误差汇总，就能反映整体拟合效果。

\begin{aligned} \text{数据}:& (x_1,y_1),(x_2,y_2) \\ \text{线性模型}:&y=wx+b \\ \text{误差}:& |y-\hat y|\\ \text{损失函数}:&\sum\limits_{k=1}^n|y_k-\hat y_k| \\ \text{均方误差(MSE)}:&\frac{1}{N}\sum\limits_{k=1}^N(y_k-\hat y_k)^2=L(w,b)\\ \text{目标}:&\text{求解让 }L\text{ 最小的 }w,b \end{aligned}

求解思路：对损失函数中的 $w$ 和 $b$ 求偏导，令导数为 0，求极值点。

实战示例：

\text{数据}:(1,1),\ (2,2),\ (3,3),\ (4,4)\\ \text{线性模型}:y=wx

\begin{aligned} L(w)&=\frac{1}{N}\sum\limits_{k=1}^N(y_k-wx_k)^2\\ &=\frac{1}{4}\left[(1-w)^2+(2-2w)^2+(3-3w)^2+(4-4w)^2\right]\\ &=\frac{1}{4}(30-60w+30w^2)\\ &=7.5-15w+7.5w^2 \\ L'(w)&=-15+15w=0 \\ w&=1 \end{aligned}

这种用线性函数拟合 $x$ 与 $y$ 关系的方法，就是机器学习中最基础的线性回归。

神经网络是由大量线性函数与非线性激活函数组合成的复杂非线性函数，对应的损失函数通常无法直接令导数为 0 求解。

假设当前 $w,b$ 为 5，损失函数为 10。 $w$ 微小变化带来损失函数的变化，就是损失对 $w$ 的偏导数， $b$ 同理。我们让 $w,b$ 往偏导数的反方向更新。

w = w - \eta\frac{\partial L(w,b)}{\partial w}\\ b = b - \eta\frac{\partial L(w,b)}{\partial b}

其中 $\eta$ 称为学习率，用来控制参数更新的步长。

这些偏导数组成的向量称为梯度。不断更新 $w,b$ 、使损失函数逐渐减小的过程，称为梯度下降。

对于深层神经网络，直接求导非常困难，但层与层之间关系简单，可以使用链式法则。

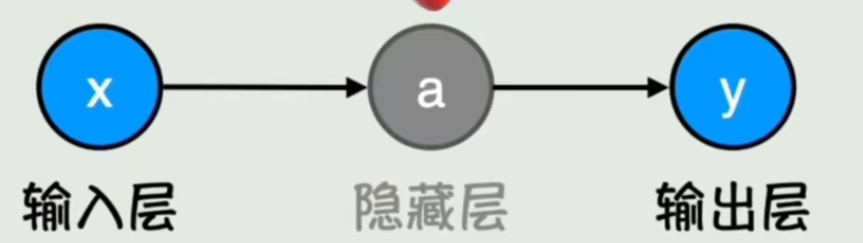F_1=g(w_1x+b_1) \\ F_2=g(w_2a+b_2) \\ F_3=(y-\hat y)^2

以 $w_1$ 为例，损失 $L$ 对 $w_1$ 的偏导：

\frac{\partial L}{\partial w_1}= \frac{\partial L}{\partial \hat y} \frac{\partial \hat y}{\partial a} \frac{\partial a}{\partial w_1}

这种分段求导再相乘的方式，称为链式法则。从输出层往输入层方向，逐层求导并更新参数，称为反向传播。

总结：

过拟合：模型在训练集上表现极好，但在未见过的测试数据上表现很差。 泛化能力：模型在未见过数据上的表现能力。

过拟合原因：模型过于复杂，把训练数据中的噪声和随机波动也学到了。

解决过拟合常用方法

从模型本身入手：

从训练阶段入手：

\text{新损失函数} = \text{原损失函数} + \lambda \sum\limits_{i=1}^N |w_i| \quad (\text{L1正则化}) \\ \text{新损失函数} = \text{原损失函数} + \lambda \sum\limits_{i=1}^N w_i^2 \quad (\text{L2正则化})

当输入输出维度很高时，用矩阵表示更简洁：

\begin{aligned} y_1&=g(w_{11}x_1+w_{12}x_2+w_{13}x_3+b_1)\\ y_2&=g(w_{21}x_1+w_{22}x_2+w_{23}x_3+b_2) \end{aligned}

写成矩阵形式：

\begin{bmatrix}y_1\\y_2\end{bmatrix}= \begin{bmatrix}w_{11}&w_{12}&w_{13}\\w_{21}&w_{22}&w_{23}\end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}+ \begin{bmatrix}b_1\\b_2\end{bmatrix}

用 $L$ 表示层数：

\mathbf{Y} = g(\mathbf{W}^{[L]}\mathbf{A}^{[L-1]}+\mathbf{b}^{[L]})

全连接层：可以整合全局信息，但参数量巨大，容易过拟合。 卷积层：用卷积核滑动提取局部特征，是 CNN 的核心。 池化层：对特征图降维，减少计算量，保留关键信息。

这种用于图像的网络结构，称为卷积神经网络 CNN。

CNN 更适合处理静态数据（如图像）。要处理时序数据（文本、语音、视频等），就需要用到 Transformer。

Lovely firefly!